Rule For Multiplying Significant Figures

2.4: Significant Figures in Calculations

Terminal updated
Salvage as PDF

Page ID: 47449

Learning Objectives

Use significant figures correctly in arithmetical operations.

Rounding

Before dealing with the specifics of the rules for determining the significant figures in a calculated result, we demand to be able to round numbers correctly. To round a number, outset determine how many meaning figures the number should have. Once you know that, round to that many digits, starting from the left. If the number immediately to the correct of the final significant digit is less than 5, information technology is dropped and the value of the last significant digit remains the aforementioned. If the number immediately to the right of the final significant digit is greater than or equal to five, the terminal meaning digit is increased by one.

Consider the measurement \(207.518 \: \text{m}\). Right now, the measurement contains half-dozen significant figures. How would we successively round information technology to fewer and fewer significant figures? Follow the procedure as outlined in Tabular array \(\PageIndex{1}\).

Table \(\PageIndex{1}\): Rounding examples
Number of Significant Figures	Rounded Value	Reasoning
6	207.518	All digits are significant
5	207.52	viii rounds the 1 up to two
iv	207.5	ii is dropped
3	208	5 rounds the seven up to eight
2	210	viii is replaced by a 0 and rounds the 0 upwards to ane
i	200	1 is replaced by a 0

Notice that the more rounding that is done, the less reliable the figure is. An approximate value may be sufficient for some purposes, just scientific piece of work requires a much college level of particular.

It is of import to be aware of significant figures when you are mathematically manipulating numbers. For case, dividing 125 by 307 on a reckoner gives 0.4071661238… to an infinite number of digits. Simply do the digits in this answer have whatever applied significant, specially when you are starting with numbers that take simply three significant figures each? When performing mathematical operations, at that place are two rules for limiting the number of pregnant figures in an answer—ane rule is for addition and subtraction, and 1 rule is for multiplication and division.

In operations involving meaning figures, the respond is reported in such a manner that information technology reflects the reliability of the least precise operation. An reply is no more than precise than the least precise number used to get the reply.

Multiplication and Partition

For multiplication or sectionalisation, the dominion is to count the number of pregnant figures in each number existence multiplied or divided and and so limit the pregnant figures in the answer to the lowest count. An case is equally follows:

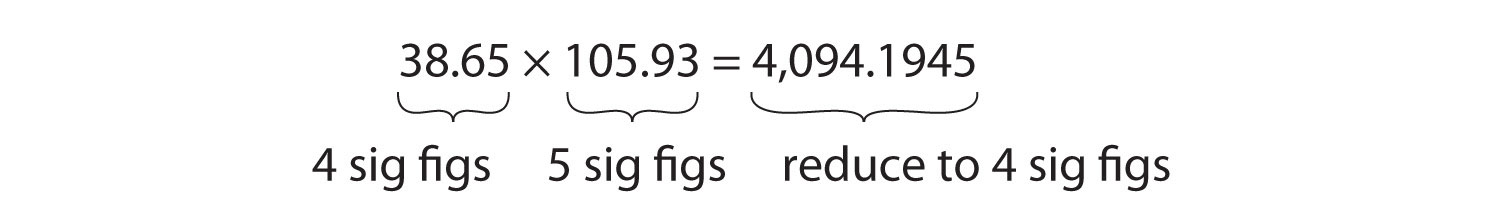
38.65 times 105.93 equals 4094.1954, which should be rounded to 4 sig figs.

The final reply, limited to four significant figures, is 4,094. The start digit dropped is 1, so we do not round upward.

Scientific notation provides a way of communicating pregnant figures without ambiguity. You simply include all the significant figures in the leading number. For example, the number 450 has two meaning figures and would exist written in scientific notation as 4.5 × x², whereas 450.0 has four meaning figures and would exist written every bit four.500 × 10ⁱⁱ. In scientific notation, all meaning figures are listed explicitly.

Example \(\PageIndex{1}\)

Write the answer for each expression using scientific notation with the advisable number of meaning figures.

23.096 × ninety.300
125 × 9.000

Solution

Tabular array with two columns and one row. The first column on the left is labeled, Explanation, and underneath in the row is an explanation. The second column is labeled, Answer, and underneath in the row is an answer.
Explanation	Reply
The calculator answer is 2,085.5688, just we demand to round it to v pregnant figures. Because the kickoff digit to exist dropped (in the tenths place) is greater than v, we round up to ii,085.6.	\(2.0856 \times 10^iii\)

Table with 2 columns and one row. The start column on the left is labeled, Explanation, and underneath in the row is an explanation. The second cavalcade is labeled, Reply, and underneath in the row is an answer.
Explanation	Respond
The calculator gives 1,125 as the answer, but nosotros limit information technology to three significant figures.	\(1.xiii \times 10^3\)

Addition and Subtraction

How are significant figures handled in calculations? It depends on what type of calculation is existence performed. If the calculation is an addition or a subtraction, the rule is as follows: limit the reported reply to the rightmost column that all numbers take significant figures in common. For instance, if you were to add 1.2 and iv.71, we annotation that the first number stops its significant figures in the tenths cavalcade, while the second number stops its significant figures in the hundredths cavalcade. We therefore limit our reply to the tenths cavalcade.

1.2 plus 4.41 equals 5.61, which should be rounded to the tenths column as 5.6

We drib the terminal digit—the 1—because it is not significant to the final answer.

The dropping of positions in sums and differences brings up the topic of rounding. Although there are several conventions, in this text we will prefer the following dominion: the last answer should be rounded upwards if the first dropped digit is v or greater, and rounded downward if the commencement dropped digit is less than 5.

77.2 plus 10.46 equals 87.66, which should be rounded to the tenths column as 87.7

Example \(\PageIndex{2}\)

13.77 + 908.226
i,027 + 611 + 363.06

Solution

a

Table with 2 columns and 1 row. The first cavalcade on the left is labeled, Explanation, and underneath in the row is an explanation. The second cavalcade is labeled, Reply, and underneath in the row is an reply.
Caption	Answer
The estimator answer is 921.996, only because 13.77 has its farthest-correct significant figure in the hundredths identify, we need to round the final answer to the hundredths position. Because the commencement digit to exist dropped (in the thousandths place) is greater than v, nosotros circular up to 922.00	\(922.00 = ix.2200 \times 10^two\)

Table with two columns and 1 row. The beginning column on the left is labeled, Explanation, and underneath in the row is an explanation. The second column is labeled, Answer, and underneath in the row is an answer.
Explanation	Answer
The calculator gives two,001.06 as the respond, merely considering 611 and 1027 has its uttermost-correct significant figure in the ones identify, the final reply must be express to the ones position.	\(ii,001.06 = 2.001 \times 10^3\)

Exercise \(\PageIndex{2}\)

Write the answer for each expression using scientific notation with the appropriate number of meaning figures.

217 ÷ 903
xiii.77 + 908.226 + 515
255.0 − 99
0.00666 × 321

Respond a:: \(0.240 = 2.40 \times 10^{-one}\)
Reply b:: \(1,437 = 1.437 \times x^3\)
Reply c:: \(156 = 1.56 \times 10^2\)
Reply d:: \(ii.14 = 2.14 \times 10^0\)

Call up that calculators exercise non understand meaning figures. You are the one who must utilize the rules of significant figures to a consequence from your calculator.

Calculations Involving Multiplication/Sectionalisation and Addition/Subtraction

In practice, chemists mostly work with a calculator and carry all digits forward through subsequent calculations. When working on newspaper, however, we ofttimes want to minimize the number of digits we have to write out. Considering successive rounding can chemical compound inaccuracies, intermediate rounding needs to exist handled correctly. When working on paper, e'er round an intermediate result and then every bit to retain at to the lowest degree ane more than digit than can exist justified and carry this number into the side by side pace in the calculation. The final answer is then rounded to the right number of significant figures at the very end.

Video \(\PageIndex{i}\): Significant figures in mixed operations (https://world wide web.youtube.com/watch?v=yBntMndXQWA).

Video \(\PageIndex{2}\): https://www.youtube.com/picket?five=__csP0NtlGI

In the worked examples in this text, we will oft show the results of intermediate steps in a adding. In doing so, we volition show the results to only the right number of meaning figures immune for that step, in outcome treating each stride as a separate calculation. This process is intended to reinforce the rules for determining the number of significant figures, but in some cases information technology may requite a final answer that differs in the final digit from that obtained using a calculator, where all digits are carried through to the last step.

Example \(\PageIndex{3}\)

2(1.008 g) + 15.99 chiliad
137.3 s + 2(35.45 s)
\( {118.7 one thousand \over two} - 35.5 thou \)

Solution

a.

Table with two columns and ane row. The offset column on the left is labeled, Explanation, and underneath in the row is an explanation for multiplication start. The second cavalcade is labeled, Answer, and underneath in the row is an answer.
Explanation	Reply
ii(i.008 g) + 15.99 g = Perform multiplication first. two (1.008 one thousand 4 sig figs ) = 2.016 g iv sig figs The number with the least number of pregnant figures is 1.008 thou; the number 2 is an verbal number and therefore has an infinite number of significant figures . And so, perform the addition. two.01six g thousandths identify + fifteen.9ix yard hundredths place (to the lowest degree precise) = 18.006 g Circular the final answer. Round the final answer to the hundredths place since 15.99 has its uttermost correct significant figure in the hundredths place (least precise).	18.01 g (rounding up)

b.

Table with two columns and 1 row. The first column on the left is labeled, Explanation, and underneath in the row is an caption for multiplication beginning. The second column is labeled, Answer, and underneath in the row is an respond.
Explanation	Respond
137.3 s + 2(35.45 s) = Perform multiplication outset. 2(35.45 s 4 sig figs ) = lxx.ninety s four sig figs The number with the least number of significant figures is 35.45; the number two is an exact number and therefore has an infinite number of significant figures. Then, perform the addition. 137.iii southward tenths identify (least precise) + 70.ninety south hundredths place = 208.xx s Round the final reply. Round the final answer to the tenths identify based on 137.3 s.	208.2 s

c.

Table with two columns and ane row. The first column on the left is labeled, Explanation, and underneath in the row is an explanation for sectionalization kickoff. The second column is labeled, Respond, and underneath in the row is an answer.
Caption	Answer
\( {118.7 yard \over 2} - 35.v g \) = Perform division get-go. \( {118.vii g \over two} \) 4 sig figs = 59.35 g 4 sig figs The number with the to the lowest degree number of significant figures is 118.vii g; the number 2 is an exact number and therefore has an space number of significant figures. Perform subtraction next. 59.35 grand hundredths place − 35.5 thou tenths identify (least precise) = 23.85 thousand Round the concluding answer. Round the final reply to the tenths place based on 35.v 1000.	23.ix 1000 (rounding upwardly)

Do \(\PageIndex{three}\)

Complete the calculations and study your answers using the correct number of significant figures.

five(1.008s) - 10.66 s
99.0 cm+ 2(5.56 cm)

Answer a: -5.62 s
Answer b: 110.2 cm

Summary

Rounding
- If the number to exist dropped is greater than or equal to 5, increase the number to its left by i (e.one thousand. 2.9699 rounded to three significant figures is ii.97).
- If the number to be dropped is less than 5, there is no alter (east.g. 4.00443 rounded to 4 meaning figures is 4.004).
The dominion in multiplication and division is that the last answer should have the same number of significant figures every bit there are in the number with the fewest significant figures.
The dominion in addition and subtraction is that the answer is given the aforementioned number of decimal places as the term with the fewest decimal places.